Kovariācija - definīcija, formula un praktiskais piemērs

Matemātikā un statistikā Finanšu pamatstatistikas jēdzieni Stingra statistikas izpratne ir ārkārtīgi svarīga, lai palīdzētu mums labāk izprast finanses. Turklāt statistikas jēdzieni var palīdzēt investoriem uzraudzīt, kovariācija ir divu nejaušu mainīgo attiecību mērs. Metrikā tiek novērtēts, cik daudz un cik lielā mērā mainīgie mainās kopā. Citiem vārdiem sakot, tas būtībā ir divu mainīgo lielumu dispersijas mērs. Tomēr metrika nenovērtē atkarību starp mainīgajiem.

Kovāriju atšķirībā no korelācijas koeficienta mēra vienībās. Vienības aprēķina, reizinot abu mainīgo lielumus. Dispersija var būt jebkura pozitīva vai negatīva vērtība. Vērtības tiek interpretētas šādi:

• Pozitīva kovariācija: Norāda, ka diviem mainīgajiem ir tendence virzīties vienā virzienā.
• Negatīva kovariācija: Atklāj, ka divi mainīgie mēdz kustēties apgrieztā virzienā.

Finansēs Finanses Finanses Raksti par finansēm ir veidoti kā pašmācības ceļveži, lai tiešsaistē apgūtu svarīgas finanšu koncepcijas savā tempā. Pārlūkojiet simtiem rakstu! , jēdziens galvenokārt tiek izmantots portfeļa teorijā. Viens no visizplatītākajiem portfeļa teorijas pielietojumiem ir diversifikācija Diversifikācijas diversifikācija ir portfeļa resursu vai kapitāla piešķiršanas metode dažādiem ieguldījumiem. Diversifikācijas mērķis ir mazināt zaudējumu metodi, izmantojot kovariāciju starp portfeļa aktīviem. Izvēloties aktīvus, kuriem savstarpēji nav augsta pozitīvā kovariācija, daļēji var novērst nesistemātisko risku.

Finanses Matemātika korporatīvo finanšu kursam pēta finanšu modelēšanai nepieciešamos finanšu matemātikas jēdzienus. Kas ir finanšu modelēšana Finanšu modelēšana tiek veikta programmā Excel, lai prognozētu uzņēmuma finanšu rādītājus. Pārskats par to, kas ir finanšu modelēšana, kā un kāpēc veidot modeli.

Kovariācijas formula

Kovariācijas formula ir līdzīga korelācijas formulai, un tā attiecas uz datu punktu aprēķināšanu no datu kopas vidējās vērtības. Piemēram, divu nejaušo mainīgo X un Y kovarianci var aprēķināt, izmantojot šādu formulu (populācijai):

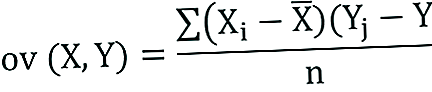
Kovariances paraugam formula ir nedaudz pielāgota:

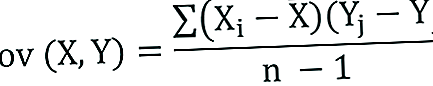
Kur:

• X_i - mainīgā X vērtības
• Jā_j- Y mainīgā vērtības
• X̄ - X mainīgā vidējais (vidējais)
• Ȳ - Y mainīgā vidējais (vidējais)
• n - datu punktu skaits

Kovariācija pret korelāciju

Kovariācija un korelācija galvenokārt novērtē saistību starp mainīgajiem. Tuvākā analoģija attiecībām starp tām ir attiecība starp dispersiju un standartnovirzi. Standarta novirze No statistikas viedokļa datu kopas standartnovirze ir noviržu lieluma mērījums starp ietverto novērojumu vērtībām.

Kovariance mēra divu nejaušo mainīgo lielumu kopējo variāciju no to paredzamajām vērtībām. Izmantojot kovariāti, mēs varam tikai novērtēt attiecību virzienu (neatkarīgi no tā, vai mainīgie mēdz pārvietoties tandēmā, vai parāda apgrieztas attiecības). Tomēr tas nenorāda ne attiecību stiprumu, ne atkarību starp mainīgajiem.

No otras puses, korelācija mēra attiecību stiprumu starp mainīgajiem. Korelācija ir kovariācijas mērogs. Tā ir bezizmēra. Citiem vārdiem sakot, korelācijas koeficients vienmēr ir tīra vērtība un netiek mērīts nevienā mērvienībā.

Attiecību starp šiem diviem jēdzieniem var izteikt, izmantojot šādu formulu:

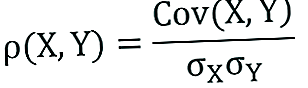
Kur:

• ρ (X, Y) - korelācija starp mainīgajiem X un Y
• Cov (X, Y) - kovariācija starp mainīgajiem lielumiem X un Y
• σ_X - X mainīgā standarta novirze
• σ_Jā- Y mainīgā standarta novirze

Kovariances piemērs

Jānis ir investors. Viņa portfelis galvenokārt izseko S&P 500 veiktspēju, un Džons vēlas pievienot ABC Corp akcijas. Pirms akciju pievienošanas savam portfelim, viņš vēlas novērtēt virziena attiecības starp akcijām un S&P 500.

Džons nevēlas palielināt sava portfeļa nesistemātisko risku. Tādējādi viņu neinteresē turēt vērtspapīrus portfelī, kas mēdz virzīties vienā virzienā.

Džons var aprēķināt kovariāciju starp ABC Corp. un S&P 500 akcijām, veicot šādas darbības:

1. Iegūstiet datus.

Pirmkārt, Jānis iegūst gan ABC Corp., gan S&P 500 skaitļus. Iegūtās cenas ir apkopotas zemāk esošajā tabulā:

2. Aprēķiniet katra aktīva vidējās (vidējās) cenas.

3. Katram vērtspapīram atrodiet starpību starp katru vērtību un vidējo cenu.

4. Reiziniet iepriekšējā solī iegūtos rezultātus.

5. Izmantojot 4. solī aprēķināto skaitli, atrodiet kovariāciju.

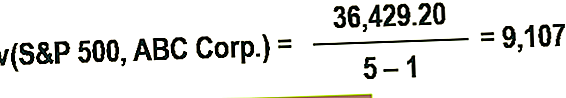
Šādā gadījumā pozitīvā kovariācija norāda, ka akciju un S&P 500 cena mēdz virzīties vienā virzienā.

Papildu resursi

Finanses piedāvā finanšu modelēšanas un vērtēšanas analītiķi (FMVA) ™ FMVA® sertifikāciju. Pievienojieties 350 600+ studentiem, kuri strādā tādos uzņēmumos kā Amazon, J.P.Morgan un Ferrari sertifikācijas programma tiem, kas vēlas virzīt savu karjeru uz nākamo līmeni. Lai turpinātu mācīties un virzīt savu karjeru, noderēs šādi finanšu resursi:

• Ieguldījumi: iesācēju ceļvedis Ieguldījumi: iesācēju ceļvedis Finanšu ceļvedis Ieguldīšana iesācējiem iemācīs ieguldīšanas pamatus un to, kā sākt darbu. Uzziniet par dažādām tirdzniecības stratēģijām un paņēmieniem un par dažādiem finanšu tirgiem, kuros varat ieguldīt.
• Negatīvā korelācija Negatīvā korelācija Negatīvā korelācija ir saistība starp diviem mainīgajiem, kas pārvietojas pretējos virzienos. Citiem vārdiem sakot, kad mainīgais A palielinās, mainīgais B samazinās. Negatīvā korelācija ir pazīstama arī kā apgriezta korelācija. Skatiet piemērus, diagrammas un
• Risks un ienesīgums Risks un ienesīgums Ieguldījumos risks un atdeve ir ļoti korelēti. Paaugstināta potenciālā ieguldījumu atdeve parasti iet roku rokā ar paaugstinātu risku. Dažādi risku veidi ietver projektam raksturīgo risku, nozarei raksturīgo risku, konkurences risku, starptautisko risku un tirgus risku.
• Riska pārvaldība Riska pārvaldība Riska pārvaldība ietver riska faktoru identificēšanu, analīzi un reaģēšanu uz tiem, kas ir daļa no biznesa dzīves. Parasti to dara ar