LASSO, kas ir saīsinājums no vismazāk absolūtā saraušanās un atlases operatora, ir statistikas formula, kuras galvenais mērķis ir pazīmju atlase un datu modeļu sakārtošana. Metodi pirmo reizi 1996. gadā ieviesa statistikas profesors Roberts Tibširani. LASSO ievada parametrus modeļa summai, piešķirot tai augšējo robežu, kas darbojas kā ierobežojums summai, lai absolūtos parametrus iekļautu pieļaujamajā diapazonā.
LASSO metode normalizē modeļa parametrus, samazinot regresijas koeficientus, dažus no tiem samazinot līdz nullei. Funkcijas izvēles fāze notiek pēc saraušanās, kur modelī tiek izvēlēta katra vērtība, kas nav nulle. Šī metode ir nozīmīga, lai samazinātu prognozēšanas kļūdas, kas ir izplatītas statistikas modeļos. Kvantitatīvā analīze Kvantitatīvā analīze ir izmērāmu un pārbaudāmu datu, piemēram, ieņēmumu, tirgus daļas un algu, vākšanas un novērtēšanas process, lai izprastu Bizness. Datu tehnoloģiju laikmetā kvantitatīvā analīze tiek uzskatīta par vēlamo pieeju pamatotu lēmumu pieņemšanā. .
LASSO piedāvā modeļus ar augstu prognozēšanas precizitāti. Precizitāte palielinās, jo metode ietver koeficientu samazināšanos, kas savukārt samazina dispersiju un samazina aizspriedumus. Tas vislabāk darbojas, ja novērojumu skaits ir mazs un pazīmju skaits ir liels. Tas lielā mērā paļaujas uz parametru λ, kas ir saraušanās kontrolējošais faktors. Jo lielāks kļūst λ, tad vairāk koeficientu ir spiesti būt nullei.
Kad λ ir vienāds ar nulli, tad modelis kļūst par parasto mazāko kvadrātu regresiju. Līdz ar to, palielinoties λ, dispersija ievērojami samazinās un palielinās arī rezultāta novirze. Lasso ir arī noderīgs rīks, lai izslēgtu visus mainīgos, kuriem nav nozīmes un kuri nav saistīti ar atbildes mainīgo.
LASSO statistiskajos lineārajos modeļos
Statistiskais modelis ir reālās dzīves problēmas matemātisks attēlojums. Modelim vajadzētu pēc iespējas tuvināt problēmu reālajai pasaulei, vienlaikus padarot to vienkāršu un viegli saprotamu. Modelis sastāv no paskaidrojošiem un atbildes mainīgiem.
The skaidrojošais mainīgais ir neatkarīgs mainīgais, kas pēc pētnieka ieskatiem. Neatkarīgie mainīgie ir modeļa ievadi, kurus pētnieks var izmērīt, lai noteiktu to ietekmi uz modeļa rezultātiem.
The reakcijas mainīgais ir atkarīgs mainīgais Atkarīgais mainīgais Atkarīgais mainīgais ir tāds, kas mainīsies atkarībā no cita mainīgā, sauktā par neatkarīgo mainīgo, vērtības. kas veido eksperimenta galveno uzmanību. Tas veido eksperimenta rezultātu, kas var būt viens rezultāts vienveidīgo modeļu gadījumā, vai, ja mainīgo variantu modeļi, vairāki rezultāti.
LASSO ir neatņemama modeļa veidošanas procesa sastāvdaļa, īpaši izmantojot funkciju izvēli. Funkciju izvēles fāze palīdz atlasīt paskaidrojošos mainīgos, kas ir neatkarīgi mainīgie un līdz ar to modeļa ievades mainīgie.
Ieejas mainīgie ir svarīgi elementi, kas nosaka modeļa iznākumu un kas palīdz izmērīt to ietekmi uz reakcijas mainīgajiem. Pareizo mainīgo lielumu izvēle nosaka modeļa precizitāti. LASSO funkciju atlases posms palīdz pareizi izvēlēties mainīgos.
Novērtējums ar LASSO
Statistikas modeļi balstās uz LASSO precīzai mainīgo atlasei un regulēšanai. Lineārās regresijas regresijas analīzē Regresijas analīze ir statistikas metožu kopums, ko izmanto, lai novērtētu attiecības starp atkarīgo mainīgo un vienu vai vairākiem neatkarīgiem mainīgajiem. To var izmantot, lai novērtētu mainīgo lielumu attiecības un modelētu turpmākās attiecības starp tiem. , piemēram, LASSO ievieš kvadrātu summas augšējo robežu, tādējādi samazinot modelī esošās kļūdas. LASSO novērtētājs ir atkarīgs no parametra λ.
Parametrs λ kontrolē saraušanās stiprumu, kur λ palielināšanās rezultātā palielinās saraušanās. Visu koeficientu summas augšējā robeža ir apgriezti proporcionāla parametram λ. Kad augšējā robeža palielinās, parametrs λ samazinās. Kad augšējā robeža samazinās, parametrs λ vienlaikus palielinās.
Augšējai robežai palielinoties uz bezgalību, parametrs λ tuvojas nullei, tādējādi pārveidojot eksperimentu parastajos vismazākajos kvadrātos, kur parametrs λ vienmēr ir vienāds ar nulli. Kad augšējās robežas koeficienti tuvojas nullei, parametra λ vērtība palielinās uz bezgalību.
LASSO ģeometrija
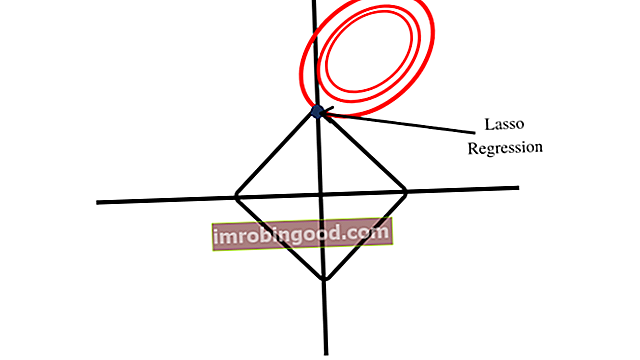
LASSO zemes gabalā veido dimanta formu savam ierobežojuma reģionam, kā parādīts zemāk esošajā attēlā. Dimanta forma ietver stūrus, atšķirībā no apļveida formas, ko veido kores regresija. Pirmā punkta tuvums stūrim parāda, ka modelim ir viens koeficients, kas ir vienāds ar nulli.
Kores regresijas ierobežojumu reģions veido apļveida formu, kurā nav stūru, kas līdzīgi tiem, kurus veido LASSO ierobežojumu reģions, kad tos uzzīmē. Tāpēc kores regresijas koeficienti nevar būt vienādi ar nulli.
Svērtais LASSO
Svērtais LASSO ir rezultāts pētniekam, kurš regresijas koeficientus soda atsevišķi. Tas nozīmē, ka tā vietā, lai visiem koeficientiem piemērotu kopīgu parametru λ, koeficientus soda individuāli, izmantojot dažādus parametrus.
Svarus var noteikt, izmantojot LASSO algoritmu, lai pareizi piešķirtu svaru precīzai modelēšanai. Līdzīgs regresijas koeficientu svērums ir kooperatīvs LASSO, kur koeficienti tiek sodīti grupās, kuras tiek uzskatītas par līdzīgām.
Papildu resursi
Finanses ir oficiālais sertificēto banku un kredītu analītiķu (CBCA) ™ CBCA ™ sertifikātu nodrošinātājs. Sertificētā banku un kredītu analītiķu (CBCA) ™ akreditācija ir globāls kredītanalītiķu standarts, kas aptver finanses, grāmatvedību, kredītu analīzi, naudas plūsmas analīzi, derības modelēšana, aizdevuma atmaksa un citas lietas. sertifikācijas programma, kas paredzēta ikviena pārveidošanai par pasaules klases finanšu analītiķi.
Lai turpinātu mācīties un pilnveidot savas zināšanas par finanšu analīzi, mēs iesakām tālāk norādītos papildu finanšu resursus:
- Prognozēšanas metodes Prognozēšanas metodes Top Prognozēšanas metodes. Šajā rakstā mēs izskaidrosim četru veidu ieņēmumu prognozēšanas metodes, kuras finanšu analītiķi izmanto, lai prognozētu nākotnes ieņēmumus.
- Neatkarīgais mainīgais Neatkarīgais mainīgais Neatkarīgais mainīgais ir ievads, pieņēmums vai draiveris, kas tiek mainīts, lai novērtētu tā ietekmi uz atkarīgo mainīgo (rezultātu).
- Vairākas lineārās regresijas Vairākas lineārās regresijas Daudzkārtējas lineārās regresijas attiecas uz statistikas paņēmienu, ko izmanto, lai prognozētu atkarīgā mainīgā rezultātu, pamatojoties uz neatkarīgo mainīgo lielumu vērtību
- Scenāriju analīze Scenāriju analīze Scenāriju analīze ir metode, ko izmanto, lai analizētu lēmumus, spekulējot ar dažādiem iespējamiem finanšu ieguldījumu rezultātiem. Finanšu modelēšanā tas

