Nejaušs mežs ir paņēmiens, ko izmanto, lai modelētu prognozes un uzvedības analīzi, un tas ir balstīts uz lēmumu kokiem. Tajā ir daudz lēmumu koku, kas atspoguļo atsevišķu gadījuma mežā ievadīto datu klasifikācijas gadījumu. Gadījuma meža tehnikā individuāli tiek ņemti vērā gadījumi, kā izvēlēto prognozi tiek ņemta tā, kurai ir balsu vairākums.
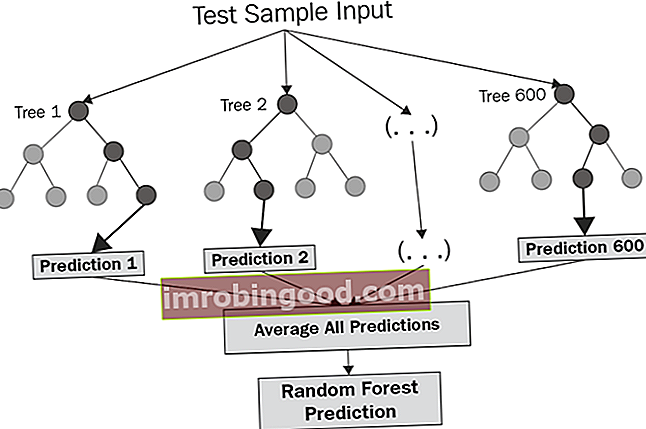1. attēls. Nejauša meža struktūra (avots)
Katrs klasifikācijas koks ņem sākotnējās datu kopas paraugus. Pēc tam pēc nejaušības principa tiek atlasītas funkcijas, kuras tiek izmantotas, audzējot koku katrā mezglā. Katru koku mežā nedrīkst apgriezt līdz vingrinājuma beigām, kad prognoze tiek sasniegta izlēmīgi. Tādā veidā nejaušs mežs ļauj jebkuram klasifikatoram ar vāju korelāciju izveidot spēcīgu klasifikatoru.
Ātrais kopsavilkums
- Nejaušs mežs ir lēmumu koku kombinācija, kuru var modelēt prognozēšanai un uzvedības analīzei.
- Lēmuma koku mežā nevar apgriezt paraugu ņemšanai un tādējādi prognozes izvēlei.
- Nejaušā meža tehnika var apstrādāt lielas datu kopas, jo tā spēj strādāt ar daudziem mainīgajiem, kas darbojas līdz tūkstošiem.
Prognozes modelēšana
Ar nejauša meža metodi var izveidot prognozēšanas modeļus, izmantojot nejaušas meža regresijas kokus, kuri parasti nav apgriezti, lai sniegtu spēcīgas prognozes. Regresijas kokiem tiek izmantota bootstrap paraugu ņemšanas metode, kuru nevajadzētu apgriezt. Optimālie mezgli tiek atlasīti no kopējiem koku mezgliem, lai izveidotu optimālu sadalīšanas pazīmi.
Nejaušās izlases metode, ko izmanto, izvēloties optimālo sadalīšanas pazīmi, samazina korelāciju un līdz ar to regresijas koku dispersiju. Tas uzlabo noteiktu koku prognozēšanas spējas mežā. Paraugu ņemšana, izmantojot bootstrap, palielina arī atsevišķu koku neatkarību.
Mainīga nozīme
Mainīgie lielumi (pazīmes) ir svarīgi nejaušam mežam, jo modeļu interpretācija ir izaicinājums, īpaši no bioloģiskā viedokļa. Naivā pieeja parāda mainīgo lielumu nozīmi, piešķirot mainīgajam nozīmi, pamatojoties uz tā biežumu, kādā visi koki to iekļauj izlasē. To var viegli sasniegt, taču tas ir izaicinājums, jo ietekme uz izmaksu samazināšanu un precizitātes palielināšanu ir lieka.
Permutācijas svarīgums ir rādītājs, kas izseko prognozēšanas precizitāti, ja mainīgie tiek nejauši izvēlēti no ārpus maisa esošiem paraugiem. Permutācijas nozīmīguma pieeja darbojas labāk nekā naivā pieeja, taču tā mēdz būt dārgāka.
Sakarā ar to, ka nejaušs mežs nespēj pietiekami labi interpretēt prognozes no bioloģiskā viedokļa, tehnika balstās uz naivajiem, vidējā piemaisījuma samazināšanās un permutācijas nozīmīguma pieejām, lai dotu viņiem tiešu interpretējamību izaicinājumiem. Trīs pieejas atbalsta prognozējošos mainīgos ar vairākām kategorijām.
Nepārtrauktu prediktoru mainīgo gadījumā ar līdzīgu kategoriju skaitu, tomēr gan permutācijas nozīme, gan vidējā piemaisījumu samazināšanās pieeja neuzrāda aizspriedumus. tirgū, kas faktiski bija nejaušības rezultāts vai neparedzēts. Mainīga atlase bieži notiek ar neobjektivitāti. Lai no tā izvairītos, jāveic apakšparaugu ņemšana bez nomaiņas, un, ja tiek izmantots nosacīts secinājums, jāpiemēro nejauša meža tehnika.
Slīpi izlases meži
Slīpi izlases meži ir unikāli ar to, ka lēmumos izmanto slīpi šķēlumus parasto lēmumu sadalījumu vietā mezglos. Slīpi meži parāda daudz pārākuma, parādot šādas īpašības.
Pirmkārt, viņi var atdalīt sadalījumus koordinātu asīs, izmantojot vienu daudzfaktoru sadalījumu, kas ietvertu tradicionāli nepieciešamos dziļi asīs izlīdzinātos sadalījumus. Otrkārt, tie ļauj samazināt lēmuma koku aizspriedumus attiecībā uz iezīmētajiem ierobežojumiem. Parastajiem asīm izlīdzinātajiem sadalījumiem būtu nepieciešami vēl divi ligzdošanas līmeņi, atdalot līdzīgas klases ar slīpajiem šķēlumiem, padarot to vieglāku un efektīvāku lietošanu.
Nejaušs meža klasifikators
Gadījuma meža klasifikators ir prognozēšanas koku kolekcija, kur katrs koks ir atkarīgs no nejauši izvēlētiem vektoriem, kas atlasīti neatkarīgi, ar līdzīgu sadalījumu ar visiem citiem nejaušā meža kokiem. Sākotnēji paredzēts mašīnmācībai, klasifikators ir ieguvis popularitāti attālās uzrādes sabiedrībā, kur tās augstās precizitātes dēļ to lieto attāli uztveramu attēlu klasifikācijā. Tas arī nodrošina pareizu nepieciešamo ātrumu un efektīvu parametru noteikšanu procesā. Gadījuma meža klasifikators sāknēt izlases paraugus, kur tiek izvēlēta prognoze ar vislielāko balsu skaitu no visiem kokiem.
Koku individualitāte ir svarīga visā procesā. Katra koka individualitāte tiek garantēta šādu īpašību dēļ. Pirmkārt, katrā koku apmācībā izlasē tiek izmantotas nejaušas apakškopas no sākotnējām apmācības izlasēm. Otrkārt, optimālais sadalījums tiek izvēlēts no neapgriezto koku mezglu nejauši izvēlētajām iezīmēm. Treškārt, katrs koks aug bez ierobežojumiem, un to nevajadzētu vispār apgriezt.
Nejaušo mežu priekšrocības
Izlases mežos ir aplēses par mainīgu nozīmi, t.i., nervu tīkliem. Viņi arī piedāvā izcilu metodi darbam ar trūkstošiem datiem. Trūkstošās vērtības tiek aizstātas ar mainīgo, kas konkrētajā mezglā parādās visvairāk. Starp visām pieejamajām klasifikācijas metodēm izlases meži nodrošina visaugstāko precizitāti.
Ar izlases meža metodi var apstrādāt arī lielus datus ar daudziem mainīgajiem lielumiem, kuru skaits ir tūkstošiem. Tas var automātiski līdzsvarot datu kopas, ja klase ir retāk sastopama nekā citas datu klases. Metode arī ātri apstrādā mainīgos, padarot to piemērotu sarežģītiem uzdevumiem.
Vairāk resursu
Finanses piedāvā finanšu modelēšanas un vērtēšanas analītiķi (FMVA) ™ FMVA® sertifikāciju. Pievienojieties 350 600+ studentiem, kuri strādā tādos uzņēmumos kā Amazon, J.P.Morgan un Ferrari sertifikācijas programma tiem, kas vēlas virzīt savu karjeru uz nākamo līmeni. Lai turpinātu mācīties un attīstīt savu zināšanu bāzi, lūdzu, izpētiet tālāk norādītos papildu finanšu resursus:
- Šķērsgriezuma datu analīze Šķērsgriezuma datu analīze Šķērsgriezuma datu analīze ir šķērsgriezuma datu kopu analīze. Aptaujas un valdības ieraksti ir daži izplatīti šķērsgriezuma datu avoti
- Klastera atlase Klastera atlase Statistikā klastera izlase ir izlases metode, kurā visa pētījuma populācija tiek sadalīta ārēji viendabīgā, bet iekšēji
- Normāls sadalījums Normāls sadalījums Normālo sadalījumu sauc arī par Gausa vai Gausa sadalījumu. Šis izplatīšanas veids tiek plaši izmantots dabas un sociālajās zinātnēs. The
- Roy drošība - pirmais kritērijs Roy drošība - pirmais kritērijs Roja drošība - pirmais kritērijs ir riska pārvaldības metode, ko investori izmanto, lai salīdzinātu un izvēlētos portfeli, pamatojoties uz kritēriju, ka varbūtības varbūtība
