Elastīgā neto lineārā regresija izmanto gan laso, gan kores tehnikas sodus, lai regulētu regresijas modeļus. Tehnika apvieno gan laso LASSO LASSO, kas ir saīsinājums no vismazāk absolūtās saraušanās, gan atlases operators, ir statistikas formula, kuras galvenais mērķis ir pazīmju atlase, regulēšana un kores regresijas metodes, mācoties no to trūkumiem, lai uzlabotu statistisko modeļu legalizāciju.
Elastīgā tīkla metode uzlabo laso ierobežojumus, t.i., ja laso ņem dažus paraugus augstas dimensijas datiem, elastīgā tīkla procedūra nodrošina “n” mainīgo skaita iekļaušanu līdz piesātinājumam. Gadījumā, ja mainīgie ir ļoti savstarpēji saistītas grupas, laso mēdz izvēlēties vienu mainīgo no šādām grupām un pārējos pilnībā ignorēt.
Lai novērstu lasos atrastos ierobežojumus, elastīgais tīkls soda mērogā iekļauj kvadrātisku izteiksmi (|| β || 2), kas, lietojot atsevišķi, kļūst par kores regresiju. Kvadrātiskā izteiksme sodā paaugstina zaudējumu funkciju pret izliekumu. Elastīgais tīkls izmanto labāko no abām pasaulēm - t.i., laso un kores regresiju.
Elastīgā tīkla metodes novērtētāja atrašanas procedūrā ir divi posmi, kas ietver gan laso, gan regresijas paņēmienus. Vispirms tā atrod kores regresijas koeficientus un pēc tam veic otro soli, izmantojot koeficientu laso veida saraušanos.
Šī metode tāpēc pakļauj koeficientus divu veidu saraušanās gadījumā. Dubultā saraušanās no naivās elastīgā tīkla versijas rada zemu prognozējamības efektivitāti un lielu novirzi. Lai labotu šādus efektus, koeficienti tiek mainīti, reizinot tos ar (1 + λ2).
Ātrais kopsavilkums
- Elastīgā tīkla metode vienlaikus veic mainīgo izvēli un regulēšanu.
- Elastīgā tīkla metode ir vispiemērotākā, ja izmēru dati ir lielāki par izmantoto paraugu skaitu.
- Grupēšana un mainīgo izvēle ir elastīgā tīkla tehnikas galvenās lomas.
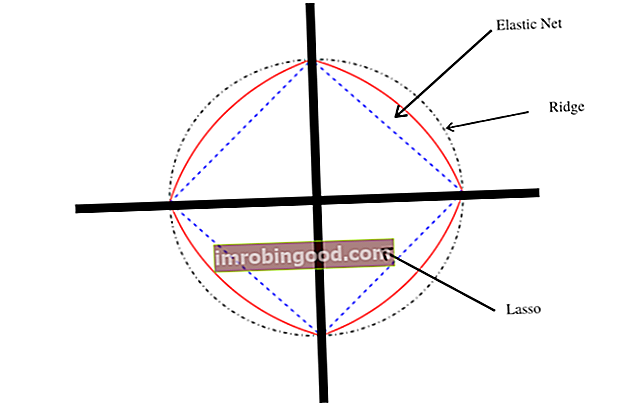
Elastīgā tīkla ģeometrija
Uzzīmējot Dekarta plaknē, elastīgais tīkls iekrīt starp kores un laso regresijas grafikiem, jo tas ir šo divu regresijas metožu apvienojums. Elastīgā tīkla sižetā virsotnēs parādās arī īpatnība, kas ir svarīga retumam. Tam ir arī stingras izliektas malas, kur izliekums ir atkarīgs no α vērtības.
Izliekums ir atkarīgs arī no grupēšanas efekta, kas atkarīgs no korelācijas Korelācija Korelācija ir statistiskais rādītājs divu mainīgo saistībai. Šo mēru vislabāk var izmantot mainīgajos lielumos, kas demonstrē lineāru saistību savā starpā. Datu piemērotību var vizuāli attēlot izkliedes diagrammā. no izvēlētajiem mainīgajiem. Jo augstāka ir mainīgo korelācija, jo lielāks ir grupēšanas efekts un līdz ar to lielāks izlasē iekļauto mainīgo skaits.
Mainīgo atlase
Lai izveidotu modeļu apakškopu, modeļa izveide prasa mainīgo izvēli. Elastīgajā tīklā tiek izmantota p >> n problēmas pieeja, kas nozīmē, ka pareģotāju skaitļu skaits ir lielāks nekā modelī izmantoto paraugu skaits. Elastīgais tīkls ir piemērots, ja mainīgie veido grupas, kurās ir ļoti korelēti neatkarīgi mainīgie. Neatkarīgais mainīgais Neatkarīgais mainīgais ir ievads, pieņēmums vai virzītājspēks, kas tiek mainīts, lai novērtētu tā ietekmi uz atkarīgo mainīgo (rezultātu). .
Mainīgā atlase ir iekļauta modeļa veidošanas procedūrā, lai palīdzētu palielināt precizitāti. Gadījumā, ja mainīgo grupa ir ļoti korelēta un izlasē tiek izvēlēts viens no mainīgajiem, visa grupa automātiski tiek iekļauta izlasē.
CATREG iekļaušana
CATREG ir algoritms, kas atvieglo mainīgo mainību - gan lineāru, gan nelineāru. Algoritms izmanto soli un splaina funkcijas, pārveidojot mainīgos lielumus vai nu nemonotoni, vai monotoni nelineārās transformācijās. CATREG var vienlaicīgi pārveidot un regulēt mainīgos nemonotoniski, neprasot vispirms mainīgos lielumus pamatfunkcijās vai fiktīvajos.
Elastīgās neto zaudējumu funkcijas var saukt arī par parasto mazāko kvadrātu regresijas zaudējumu funkcijas ierobežoto tipu. CATREG algoritms ir iestrādāts elastīgajā tīklā, kas uzlabo iegūtā algoritma efektivitāti un vienkāršību. Salīdzinājumam - elastīgais tīkls pārspēj laso, kas pats par sevi sniedz augstumu regresijas efektivitātes un vienkāršības ziņā.
Elastīgā tīkla regulēšana
Regulēšanas procedūras laikā l1 sadaļa soda veido retu modeli. No otras puses, soda kvadrātiskais posms padara l1 daļa stabilāka normalizācijas ceļā, novērš atlasāmo mainīgo lieluma ierobežojumu un veicina grupēšanas efektu.
Grupēšanas efekts palīdz mainīgos viegli identificēt, izmantojot korelāciju. Tas uzlabo paraugu ņemšanas procedūru. Tas arī palielina atlasīto mainīgo skaitu, jo, ja viens mainīgais tiek atlasīts ļoti korelējošā grupā, visi pārējie šīs grupas mainīgie tiek automātiski pievienoti paraugam.
Efektīvie brīvības pakāpes
Efektīvas brīvības pakāpes mēra modeļa sarežģītību. Novērtējot vai precīzi paredzot modeļa pielāgošanu, svarīgas ir brīvības pakāpes. Brīvības pakāpes tiek iekļautas arī lineāro gludumu apguvē. Jebkurā metodē, kas saistīta ar l1 sods, modeļu nelineārais raksturs izaicina analīzi.
Elastīgo tīklu var izmantot arī citās lietojumprogrammās, piemēram, reti sastopamajā PCA, kur tas iegūst galvenos komponentus, kurus modificē retas slodzes. Otrs pielietojums ir kodola elastīgajā tīklā, kur klases kodola mašīnu ģenerēšana notiek ar atbalsta vektoriem.
Papildu resursi
Finanses piedāvā sertificētu banku un kredītu analītiķu (CBCA) ™ CBCA ™ sertifikātu sertificēto banku un kredītu analītiķu (CBCA) ™ akreditācija ir globāls kredītiķu analītiķu standarts, kas aptver finanses, grāmatvedību, kredītu analīzi, naudas plūsmas analīzi, paktu modelēšanu, aizdevumu atmaksas un vairāk. sertifikācijas programma tiem, kas vēlas karjeru pārcelt uz nākamo līmeni. Lai turpinātu mācīties un attīstīt savu zināšanu bāzi, lūdzu, izpētiet tālāk norādītos papildu finanšu resursus:
- Lēmumu koks Lēmumu koks Lēmumu koks ir atbalsta rīks ar kokam līdzīgu struktūru, kas modelē iespējamos rezultātus, resursu izmaksas, komunālos pakalpojumus un iespējamās sekas.
- Atkarīgais mainīgais Atkarīgais mainīgais Atkarīgais mainīgais ir tāds, kas mainīsies atkarībā no cita mainīgā, sauktā par neatkarīgo mainīgo, vērtības.
- Daudzkārtēja lineārā regresija Daudzkārtēja lineārā regresija Daudzkārtēja lineārā regresija attiecas uz statistikas metodi, ko izmanto, lai prognozētu atkarīgā mainīgā rezultātu, pamatojoties uz neatkarīgo mainīgo lielumu vērtību
- Overfitting Overfitting Overfitting ir statistikā lietots termins, kas attiecas uz modelēšanas kļūdu, kas rodas, ja funkcija pārāk cieši atbilst noteiktam datu kopumam

